Ку́бик Ру́біка (часто: кубик-рубік) — механічна головоломка, яку винайшов у 1974 році угорський скульптор, винахідник Ерньо Рубік.

Ерньо Рубік назвав свій винахід «Магічний куб», але у 1980 році компанія Ideal Toys перейменувала головоломку за іменем винахідника і цього ж року виграла німецьку нагороду «Гра року» (Spiel des Jahres).

В усьому світі вже продано понад 300 млн. екземплярів іграшки.

Історія

Винахід

У березні 1970 Гаррі Д. Нікольс винайшов і пізніше запатентував у США перший кубик розміром 2×2×2 (англ. “Puzzle with Pieces Rotatable in Groups”). Кубика Нікольса зберігав цілісність за допомогою магнетизму. За ним послідкував Франк Роксі, який отримав британський патент на кубик розміром 3х3х3 (англ. “Spherical 3x3x3”).

Рубик винайшов свій «Магічний Кубик» у 1974 році та здобув угорський патент HU170062 роком пізніше, але не подав на отримання міжнародних патентів. Перша пробна партія продукту була запущена в кінці 1977 і надійшла у Будапештські іграшкові магазини. Пластикові елементи, які були покладені в основу виробу, були значно дешевші ніж магніти за дизайном Нікольса. У вересні 1979 року угода з Ideal Toys вивела «Магічний Кубик» у західний світ, і головоломка дебютувала на іграшковому ринку у січні та лютому 1980 року.

У 1982 році компанія Moleculon Research Corp, асигнована Нікольсом, подала в суд на Ideal Toys за недотримання патентного договору. За рішенням суду кубик Кишеньковий кубик 2х2х2 порушував патент Нікольса, але кубик Рубіка 3х3х3 залишався патентованим винаходом Е.Рубіка.

Популярність

З 1980 по 1982 роки було продано більше 1 млн. кубиків Рубіка. Ideal Toys випускала «Інформаційний бюлетень кубика Рубика» з 1980 по 1983 роки.

Незабаром з’явились схожі головоломки, як від самого Рубіка, так і з інших джерел, включаючи кубик 4х4х4 — «Помста Рубіка». Є також варіанти розмірів 2х2х2 та 5х5х5 («Кишеньковий кубик» та «Професорський кубик», відповідно) та головоломки інших форм, таких як піраміда і тетраедр.

У травні 2005 грецький винахідник П. Вердес (Panagiotis Verdes) сконструював кубик розміром 6х6х6. 23 травня 2006 року Френк Моріс, світовий чемпіон зі швидкубінгу, протестував цю версію. Йому вистачило 5 хвилин та 37 секунд на розв’язок головоломки. Раніше кубик Рубіка він розв’язував за 15 секунд, кубик 4х4х4 – за 1 хв. 10 с., кубик 5х5х5 – за 1 хв. 46.1 с. У липні 2006 року П. Вердес успішно сконструював кубик 7х7х7. 27 жовтня 2006 року було випущено відео розв’язку Морісом цієї головоломки. Він розв’язав її за 6 хв. 29.31 с.

В 1994 році Мілінда Грін, Дон Хатч та Джей Бекенільт (Melinda Green, Don Hatch, Jay Berkenilt) створили 4-х вимірний 4х4х4х4 аналог кубика. Кількість можливих станів цього кубика перевищує кількість атомів у відомому всесвіті. На січень 2007 року лише 55 людям вдалося його розв’язати. У 2006 році Ройс Нельсон та Чарлі Невіл (Roice Nelson, Charlie Nevill) створили 5-ти вимірну модель 5х5х5х5х5. На січень 2007 її розв’язало лише 7 людей.

Механізм

З центральних і бокових елементів з внутрішньої сторони фрагмент вирізаний таким чином, що утворюється порожнина у вигляді об’єднання трьох циліндрів. Крім того, на бокових і кутових елементах є виступи особливої форми. Ці виступи утворюють фрагмент циліндра, який щільно входить в порожнину. Завдяки такій конструкції, грані кубика вільно обертаються.

В центрі конструкції замість “невидимого кубика” знаходиться тривимірна хрестовина, на якій вільно обертаються центральні елементи. Всі інші елементи тримаються один за одного, входячи виступами в вищеописану виїмку.

Орієнтовні безмасштабні креслення

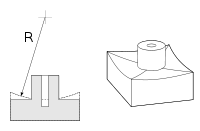
Центральний елемент

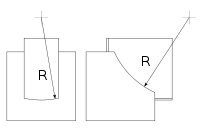
Боковий елемент

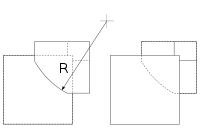
Кутовий елемент

Комбінаторика

Кубик Рубіка може мати (8! × 38−1) × (12! × 212−1)/2 = 43 252 003 274 489 856 000 різних позицій (комбінацій), або приблизно 4.3 × 10^19. Незважаючи на таку величезну кількість комбінацій станів, будь-який кубик Рубіка можна розв’язати не більше ніж за 20 рухів.

Для порівняння, якщо викласти всі комбінації кубика Рубіка за кінці вздовж однієї лінії, то довжина цієї лінії становитиме 261 світлових років.

Існує (8! × 38) × (12! × 212) = 519 024 039 293 878 272 000 ймовірних варіантів розміщення елементів кубика, але лише один із дванадцяти можна отримати на практиці. Причиною цього є те, що неможливо рухати бокові елементи. Отже існує 12 можливих наборів досяжних конфігурацій, які також називають орбітами.